Solving non-linear equations, which are those where the exponent on the variable is not 1, is very common in calculus. Knowing how to tackle these can make a big difference in terms of how many marks you get on a problem. Here is a good example that I will solve.

First few steps might be obvious. I need to move the "-1" to the right-side of the equation, making it a "+1". Then I need to divide both sides by 5. Most students can follow these and here is what it looks like in practice.

The next step is the most challenging one for students. It helps to review your exponent laws.
Think about what number do you need to multiply by 3/4 to make it a 1? That answer is 4/3. After all, (3/4) (4/3) = 1. So we are going to raise both sides to the power of 3/4.
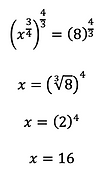
A few notes about the few steps above:
On the left-side I multiplied the two exponents as we had 2 exponents on x.
On the right-hand side it didn't make sense for me to keep it as 8 to the power of 4/3.
I had to re-write it using square root form. The denominator of the fractions, which is 3, becomes the root number and then the numerator, which is the 4, becomes the exponent number.